هدف سنجی ، بیان قوانین مدل دینامیکی ، بیان محدودیت ها در تئوری کنترل بهینه به منظور پیاده سازی در پر
به منظور بیان بهینه سازی در پروژه ها و پایان نامه های کنترلی نیاز به گذر از گام های زیر امری ضروری است :
1. در اولین گام بایستی مدل سیستم شناسایی شود ، در برخی کاربردها مدل سیستم به صورت خطی بیان می شود و یا به منظور ساده سازی مسئله ابتدا خطی سازی صورت می گیرد ، در این حین هدف گذاری کار ساده خواهد بود و معمولا تابع هدف براساس هزینه و مقدار خطا (که عموما خطای ماندگار در نظر گرفته می شود) بیان می شود . در این حالت ماتریس های وزنی مربعی به این منظور استفاده می شود که ماتریس های Q و R برای نامگذاری آن ها استفاده می شود .
در تئوری کنترل با بزرگ انتخاب نمودن ماتریس های قطری معرفی شده اهمیت هزینه و خطای قابل قبول برای متغیرهای حالت تعیین می شود .
اما در مدل های غیرخطی وضعیت متفاوت است ، در این حالت نیاز است تا از روش های غیرخطی که برمبنای پونتریاگین بیان می شود برای این منظور استفاده کرد . روش های بکار رفته در این حالت براساس برنامه نویسی غیرخطی می باشد و روش های بکار رفته لزوما مینیمم مطلق را در سیستم تعیین نمی کنند .
2. گام دوم در حل مسائل بهینه سازی مربوط به هدف سنجی می شود ، اینکه در این پروژه هدف شما از بهینه سازی چیست ؟
- کاهش زمان پاسخ دهی
- کاهش انرژی کنترلی
- کاهش نوسانات سیستم
- کاهش خطای حالت ماندگار
تعیین هدف بصورت مستقیم در تعیین تابع هزینه تاثیرگذار خواهد بود ، بالتبع در مورد اول تابع هزینه از انتگرال مجذور یا قدرمطلق عبارت زمان ، در مورد دوم قدرمطلق یا مجذور سیگنال کنترلی (مجذور به معنای انرژی نزدیکتر خواهد بود) ، مورد سوم مجموع تغییر علامت تفاضلات خروجی ها از خروجی های متناظر و در مورد چهارم مجموع تفاضلات بر روی خروجی ها تشکیل می شود .
3. بیان محددیت ها یکی از اساسی ترین گام های بهینه سازی است ، مسلما مسئله بهینه سازی بخودی خود بهترین پاسخ برمبنای تابع هزینه را به شما خواهد داد اما آیا این پاسخ قابل قبول است ؟ به عنوان مثال در پروژه ها و پایان نامه های مرتبط با رباتیک زاویه محرک ها (actuator) دارای یک محدودیت می باشد و نمی تواند تمام زاویه از -180 تا 180 را داشته باشد ، در برخی مسائل پیچیده تر نظیر مسائل فضاپیما این محدودیت ها به صورت عبارت جبری غیرخطی بیان می شوند که همگی در شروط مسئله بهینه سازی پونتریاگین بایستی در نظر گرفته شوند . (محدودیت های دینامیکی به عنوان قوانین افزوده در سیستم در نظر گرفته می شوند) .
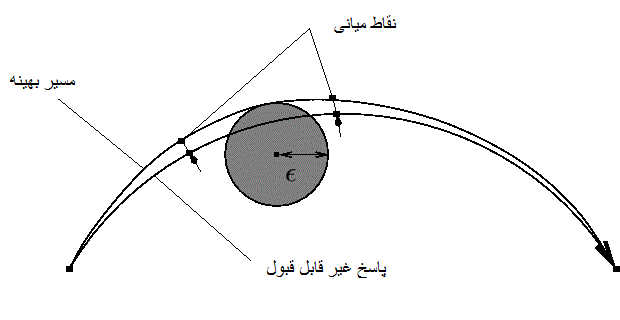
شکل عبور فضاپیما از نقطه ابتدایی به انتهایی براساس تئوری کنترل بهینه
همانگونه که در شکل مشخص است پاسخ دوم بهینه تر است ولی غیرقابل قبول که این مسئله در بیان مسئله به صورت یک معادله جبری بیان می شود ، حال آنکه اگر این تغییر متغیر با زمان باشد (گوی دارای حرکت دینامیکی باشد) نیاز به بیان معادله حالت به صورت دینامیکی می باشد .