کاربرد روش های تطبیقی در ریزشبکه ها به صورت تحلیلی
سیستم های کنترل تطبیقی برای مدل هایی که با تغییرات پارامتر (پارامترهای) سیستم همراهند کاربرد دارد ، در تئوری کنترل از این دست مدل ها با عنوان مدل های نامعین تعبیر می شود ، چیزی که مسئله اساسی در این حین می باشد بحث حساسیت سیستم به پارامتر نامعین مورد نظر است ، در یک مدل دینامیکی همراه با کنترلر ، برخی از پارامترها حساسیت بالایی روی سیستم ایجاد می کنند و در نتیجه تغییر آن ها باعث نوسانات و یا حتی تغییر در مقادیر ماندگار سیستم نیز شود .
یک ریزشبکه مجموعه ای از سیستم های تولید پراکنده تجدیدپذیر می باشد که در لینک های AC و DC با یکدیگر کوپل شده اند و بارهای خطی و غیرخطی را تغذیه می کنند ، در این بین پارامترهای نامعینی همچون میزان توان تولیدی هر یک از منابع احتمالی نظیر توربین بادی و سلول خورشیدی یا سیستم ذخیره ساز به لحاظ در نظر گرفتن سایز و عمر سلول ها یا میزان بار تغذیه شده همگی می توانند همراه با نامعینی باشند .
نامعینی های ذکر شده در مبحث سیستم های قدرت تحت عنوان قابلیت اطمینان سیستم در حفظ متغیرهای ولتاژ و فرکانس بیان می شود به گونه ای که هر اندازه شاخص متشکل از متغیرهای اساسی ولتاژ و فرکانس به مقادیر قابل اطمینان خود نزدیک باشند .
در واقع تابع هزینه سیستم ریزشبکه از میزان هزینه واحدها و تنظیم بودن مقادیر ولتاژ و فرکانس با مقادیر رفرنس بیان می شود .
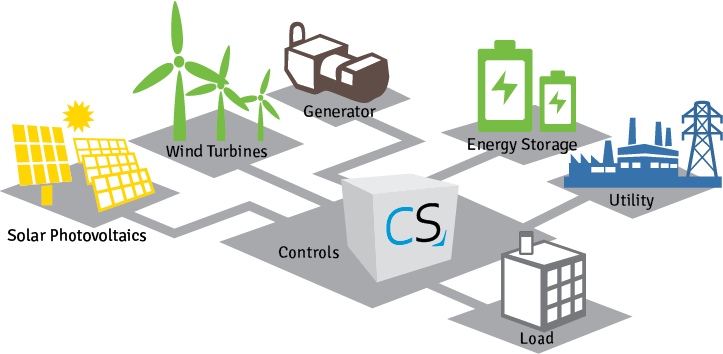
آنچه در مفهوم شماتیکی بیان شد در قضیه بررسی تحلیلی سیستم های ریزشبکه با استفاده از مدل های خطی برای سیستم های هیبریدی بیان می شود و نیاز است تا در طراحی بتوانیم پارامترهای نامعین را همگام با سیستم تخمین زده و در سیستم کنترلی از مقادیر بروز استفاده شود .
البته راه حل دیگر در بررسی این موضوع با استفاده از تئوری کنترل مقاوم بیان می شود که در آن جا این مسئله با در نظر گرفتن بازه ها برای مقادیر نامعین کران دار قابل حل می باشد .
مبحث ریزشبکه ها از جمله مباحث جدیدی می باشد که در آن ارتباط بین قدرت و کنترل بسیار محسوس می باشد . در پایان نامه های جدید و پروژه های بررسی شده در هر دو زمینه قدرت و کنترل ارائه راه حل در خصوص نامعینی های پارامتری سیستم های هیبریدی از مباحث جدید و کارامد می باشد که توجهات زیادی را به خود جلب کرده است .
در ادامه مطلب چندین مقاله جدید در موضوعیت این مسئله قرار داده شده است .