کنترل بهینه یکی از شاخه های اساسی در مبحث کنترل سیستم های مقید و غیرمقید می باشد ، این مبحث هم در ساختارهای دارای معادلات دینامیکی مشخص و هم در ساختارهای عددی دارای کاربرد می باشد . بحث کنترل بهینه در ساده ترین شکل خود که دارای هیچ قید بخصوصی نمی باشد می تواند از رگولاتور مربعی خطی موسوم به LQR شروع شده و سپس به روش های پونتریاگین و یا معادلات ریکاتی در سیستم های با نقطه انتهای مشخص و قیود خطی برسد .

آنچه که گفته شد تنها برای سیستم های با معادلات دینامیکی مشخص و خطی می باشد ، حال آنکه در سیستم های غیرخطی این مسئله با چالش بیشتری روبروست و در موارد بسیاری یافتن یک مسیر بهینه در میان قیود خطی و غیرخطی ارائه شده برای آن غیرممکن و یا حداقل بسیار دشوار می باشد . 

مسیریابی بهینه برای اندافکتور یک ربات ، مسیر بهینه برای یک موبایل ربات و یا یک جسم پرنده مانند کوادروتور و حتی سفینه های فضایی که دارای قیود هولونومیک و غیرهولونومیک می باشند از این دست مسائل بهینه سازی محسوب می شوند .

آنچه در سیستم های جدید بیشتر رخ می دهد وجود دینامیک در قیود سیستم می باشد ، حال آنکه این دینامیک می تواند به خودی خود شناخته شده نباشد و نیاز به شناسایی پارامترهای آن نیز باشد که محققین در این مسئله را به سمت استفاده از سیستم های هوشمند که ویژگی های تطبیقی در مسئله مسیریابی بهینه (optimal path planning) را نیز وارد کار کند را ضروری می سازد .

شاید بتوان گفت بهینه سازی پیچیده ترین مسئله کنترل می باشد که در تمامی سیستم های خطی و غیرخطی می توان به کار بیاید .

در مسائل مرتبط با بهینه سازی و انجام پروژه های و پایان نامه های مرتبط با آن کار کردن با توابعی که حل معادلات دیفرانسیل پیچیده آن را ممکن کند ضروری است و نیاز است تا از توابع سیمبولیک متلب در این زمینه استفاده شود .

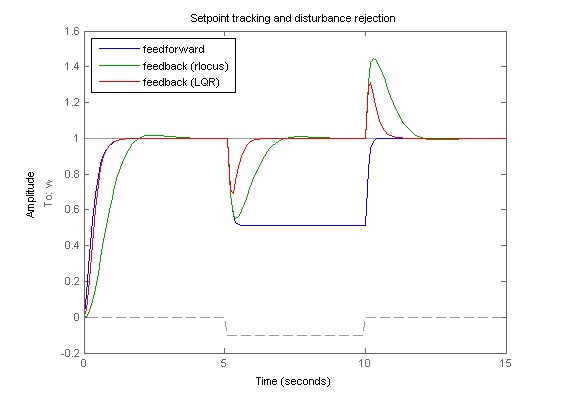
شکل بالا اهمیت یک کنترل بهینه موردی در یک موتور DC نشان می دهد . تنظیم مناسب تابع هزینه می تواند یک مصالحه مناسب برای انرژی کنترلی صرف شده و نتیجه گرفته شده از خروجی مسئله از لحاظ کیفیت کنترل را نشان دهد .

 -.-.-.-.-.-.-.-.-.-.-. -.-.-.-.-.-.-.-.-.-.-. -.-.-.-.-.-.-.-.-.-.-. -.-.-.-.-.-.-.-.-.-.-. -.-.-.-.-.-.-.-.-.-.-.-.-.-.