طراحی کنترل کننده با رویکرد مقاوم برای ریزشبکه
سیستم های قدرت نظیر ریزشبکه ها ، درایوها ، پایدارساز های سیستم قدرت و مبدل ها همواره در ساختار خود با عدم قطعیت مواجه هستند و طراحی کنترل کننده هایی نظیر PID و یا فازی می توانند بصورت محلی پایداری این سیستم ها را تضمین نمایند . به عنوان نمونه یک ریزشبکه بر روی مبدل منابعی نظیر باتری می تواند نامعین در نظر گرفته شود و سیستم کنترل مورد نظر باید بتواند این محدوده نامعینی را پوشش دهد .
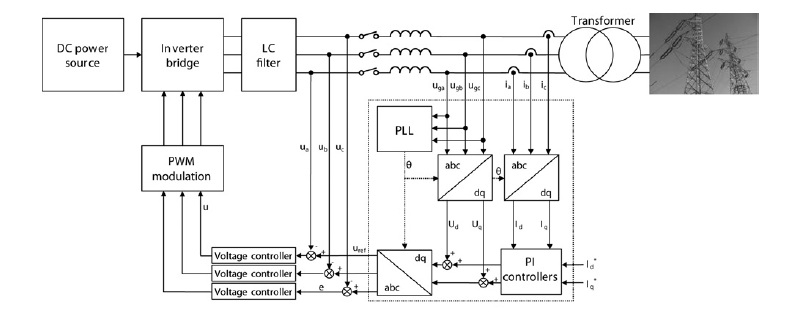
در شکل بالا یک ریزشبکه نوعی که در می تواند در حالت اتصال به شبکه و یا جزیره ای قرار داشته باشد نمایش داده شده است . در این طراحی می توان مقاومت دیده شده از سمت مبدل و همچنین مقاومت شبکه و مقادیر فیلتر شکل دهی مبدل DC به DC خروجی را نامعین و همراه با عدم قطعیت در نظر گرفت ، از دیگر سو این مقادیر همواره تحت تاثیر منابع شبکه و مقاومت دیده شده از این منابع به خودی خود دارای نامعینی می باشند . به این منظور می توان از ساختارهای مقاوم در این گونه مدل ها بهره برد .
به منظور طراحی کنترل کننده مقاوم برای تمامی ساختارها ابتدا نیاز است تا مدل فضای حالت بخش همراه با عدم قطعیت بیان شود . به طور مثال در مورد ریزشبکه این بخش شامل فیلتر و مقاومت های دیده شده از سوی مبدل و ریزشبکه می باشد .
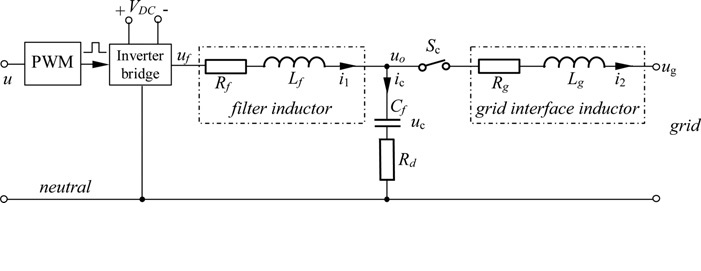
در شکل بالا این مسئله نشان داده شده است ، حال در این شرایط می توان با بررسی قوانین مداری معادل فضای حالت سیستم را بدست آورد که با توجه به سه عنصر ذخیره ساز از مرتبه 3 خواهد بود .
پس از این گام بنابر روش های معرفی شده در تئوری مقاوم بایستی مدل تعمیم یافته (Generalized) را تشکیل داده و با استفاده از روش های H2 و یا H اینفینیتی نسبت به طراحی بخش مقاوم اقدام نمود .